Artigo escrito com a colaboração de Laura Kubitschek e Joziane Vieira
Notícias sobre as vacinas contra o coronavírus tomaram conta dos jornais nos últimos meses. Junto dessas notícias vieram também muitos testes estatísticos e termos técnicos da área para comprovar a eficácia das vacinas. Mas você já conhecia esses termos? Tem ideia de como foi calculada a eficácia?
No artigo de hoje vamos explicar um pouco mais sobre a estatística por trás da aprovação das vacinas. Continue lendo para saber mais sobre essa área da ciência responsável por salvar vidas.
Há algumas semanas, a Anvisa deu uma das notícias mais aguardadas dos últimos meses. “A Gerência-Geral de Medicamentos recomenda a aprovação do uso emergencial da vacina Coronavac, condicionada ao monitoramento das incertezas e reavaliação periódica.”
Mais de 10 meses depois do início da pandemia de coronavírus, essa notícia foi muito animadora. E só foi possível pelo esforço de muitas pessoas entre cientistas, profissionais da saúde e estatísticos também!
Assim como em várias outras áreas do conhecimento, na área da saúde é preciso realizar experimentos, coletar dados e analisar quais os impactos de diferentes tratamentos no bem-estar dos pacientes. Com a vacina para o coronavírus não poderia ser diferente. E, para concluir se um imunizante é eficaz, é preciso realizar análise de dados com alguns métodos estatísticos.

Como se calcula a eficácia de uma vacina?
O processo de criação de uma vacina começa com a definição da melhor composição para o imunizante. Essa etapa é realizada com experimentação in vitro que depois é testada em animais para comprovar os dados colhidos no laboratório. O teste em animais checa a segurança e a potência imunológica da vacina. Essa fase é conhecida como pré-clínica.
Em seguida passamos para a fase clínica onde começam os testes em humanos. Essa fase é dividia em 4 partes:
- A fase 1 para testar a segurança e potência da vacina destinada apenas para pessoas sadias e que estão mais expostas ao vírus.
- A fase 2 em que um grupo maior de pessoas é testado para expandir as observações sobre a imunogenicidade da vacina.
- A fase 3 em que são realizados estudos de eficácia com um número bem maior de pessoas, geralmente de 30 a 60 mil indivíduos.
- A fase 4 quando a vacina obtém registro sanitário e é disponibilizada para a população.
Os quatro laboratórios que já chegaram à fase 3 (até a data da publicação desse artigo) e apresentaram seus resultados de eficácia foram o Instituto Gamaleya, ligado ao Ministério da Saúde da Rússia; a parceria entre Pfizer e Biontech; a empresa americana Moderna e a parceria entre Oxford e Astrazeneca. Todos publicaram taxas de eficácia acima de 90%, mas como essas taxas são calculadas?
Com os dados da fase 3 em mãos, precisamos determinar:
- V: quantas pessoas tomaram a vacina
- P: quantas tomaram o placebo
- v: quantas pessoas vacinadas contraíram a doença
- p: quantas pessoas que tomaram placebo contraíram a doença
Com esses números fazemos o seguinte cálculo:
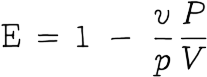
O que a eficácia realmente significa?
Existe um erro comum na hora de interpretar os dados de eficácia da vacina: um imunizante com 95% de eficácia protege 95% da população. Isso não é verdade. A vacina protege 95% das pessoas que pegariam o vírus caso não fossem vacinadas.
Isso porque o cálculo de eficácia da vacina considera a razão entre as pessoas infectadas pelo vírus com e sem a vacina. O cálculo descarta quem não contraiu o vírus. E a eficácia da vacina é medida dessa forma porque o intuito é proteger aquelas pessoas que teriam ficado doentes, não as que ficariam saudáveis mesmo sem vacina.
Num exemplo prático, se vacinássemos uma população de 100 mil pessoas e a vacina protegesse 95% delas – o que, de novo, não acontece – isso deixaria 5 mil pessoas doentes.No entanto, não são todas as 100 mil pessoas que tomariam contato com o vírus. Na realidade, de acordo com as pesquisas, cerca de 1% das pessoas que tomaram placebo ficaram doentes. Então, em um grupo de 100 mil, teríamos 1000 pessoas doentes, com a vacinação esse número cai em 95%. Ou seja, apenas 50 pessoas doentes em um grupo de 100 mil. Isso representa um impacto gigantesco no avanço do vírus.
Qual a diferença entre eficácia e efetividade?
O cálculo da eficácia é muito importante na fase 3 e quando indica resultados promissores leva a vacina para a fase 4. Mas existem outros obstáculos para que ela chegue até as pessoas que precisam. Por isso, depois que começa a ser aplicada em larga escala podemos calcular também a efetividade, que considera outras condições de acesso ao imunizante.
Vacinas que demandam uma logística mais complexa podem demorar mais a chegar, estragar no caminho ou ser difíceis de armazenar por um longo período. Se precisar de geladeiras com temperaturas muito baixas, por exemplo, é possível que nem todos os lugares tenham a infraestrutura necessária para realizar a vacinação. Diminuindo a quantidade de pessoas que recebem a injeção. O custo também é um problema que deve ser considerado já que reduz o acesso ao imunizante.
O cálculo da efetividade é um pouco diferente, precisamos considerar os seguintes números:
- A: número de pessoas vacinadas que ficaram doentes
- B: número de pessoas vacinas que não ficaram doentes
- C: número de pessoas não vacinadas que ficaram doentes
- D: número de pessoas não vacinadas que não ficaram doentes
Efetividade = 1 – (A x D)/ C x B
Como foi calculada a eficácia da vacina coronavac?
Durante a apresentação da Anvisa para a autorização de uso emergencial da vacina Coronavac, foram mencionadas duas formas de calcular a eficácia de uma vacina, apesar de apenas uma delas ter sido discutida. Em ambos casos, a eficácia é encontrada subtraindo a razão de risco do número 1, no entanto, a forma que essa razão é calculada varia nos dois métodos.
A maneira de calcular a eficácia de uma vacina utilizada pela Anvisa na divulgação dos resultados é feita ajustando um modelo de regressão de Cox. A partir desse método é possível considerar o tempo que o participante ficou exposto ao vírus a partir de 2 semanas após ter recebido a segunda dose da vacina/placebo até sua infecção.
Nesse cenário de pesquisa clínica e epidemiológica, o modelo de Cox é útil para descrever a relação entre o tempo até a contaminação por Covid-19 e um conjunto de covariáveis, sendo a principal delas o grupo do voluntário, ou seja, se ele recebeu vacina ou placebo. Dessa forma, temos a seguinte expressão:
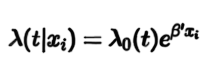
em que xi=(x1i,x2i, … , xpi)é um vetor que representa as p covariáveis presentes no modelo, =(1, 2, … , p)’ é o vetor de coeficientes do modelo, 0(t) é uma função de risco de contaminação base que não depende das covariáveis e i=1,2, …, n identifica os participantes da pesquisa.
Esse modelo, que é semi-paramétrico, tem como única suposição a proporcionalidade das taxas de risco, isto é, a razão de risco (hazard ratio) da ocorrência de infecção é constante ao longo do tempo.
Os parâmetros do ajuste são estimados pelo método de máxima verossimilhança parcial, sendo também possível realizar testes de hipóteses para testar se são significativamente diferentes de 0. Para a aprovação da Coronavac, a Anvisa realizou os testes de Wald, Escore e Razão de verossimilhanças, e todos eles apresentaram valor-p inferior ao nível de significância fixado, tendo assim evidências significativas de que o coeficiente testado era diferente de 0.
Testing Global Null Hypothesis: BETA = 0
| Teste | Chi-Square | DF | Pr > ChiSq |
| Likelihood Ratio | 29.3186 | 1 | <.0001 |
| Score | 28.8312 | 1 | <.0001 |
| Wald | 27.6725 | 1 | <.0001 |
Por fim, uma vez que foi estimado o parâmetro ligado à covariável que representa se o voluntário recebeu placebo ou vacina, sendo a categoria placebo usada como referência, é possível determinar a razão de risco apenas calculando o exponencial do valor estimado. Uma vez que se tem a razão de risco, basta subtrair esse valor de 1 para encontrar a eficácia.
| Parameter | DF | Parameter Estimate | Standard Error | Chi-Square | Pr > ChiSq | Hazard Ratio | 95.42% Hazard Ratio Confidence Limits | Label | |
| RNDGRPN | VACCINE | 1 | -0.70090 | 0.13324 | 27.6725 | <.0001 | 0.496 | 0.380 to 0.647 | RNDGRPN Vaccine |
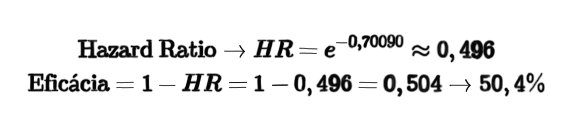
Como calcular a eficácia da vacina usando R?
Para ilustrar essas duas formas de cálculo de eficácia que apresentamos, iremos utilizar o banco de dados brcancer do pacote simsurv. Esse banco faz parte de um estudo alemão sobre câncer de mama, que investiga a eficácia de um tratamento hormonal, cenário análogo à eficácia de uma vacina.
Com esse intuito, carregamos o pacote com os dados (simsurv) e o pacote tidyverse para fazer algumas manipulações nos dados, como mudar os nomes das colunas para português. Abaixo, tem-se as primeiras 5 linhas do banco.
library(tidyverse)
library(simsurv)
dados %
transmute(tratamento_hormonal=hormon,
tempo_recorrencia=rectime,
censura_recorrencia=censrec)
dados %>%
DT::datatable(rownames = FALSE,
options =
list(language =
list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Portuguese-Brasil.json'),
columnDefs = list(list(width = '170px', targets = "_all", className = 'dt-center'))
))
| tratamento_hormonal | tempo_recorrencia | censura_recorrencia |
| 0 | 1814 | 1 |
| 1 | 2018 | 1 |
| 1 | 712 | 1 |
| 1 | 1807 | 1 |
| 0 | 772 | 1 |
| … | … | … |
Dicionário dos dados
- tratamento_hormonal: variável binária que indica se a paciente recebeu o tratamento hormonal (1) ou não (0);
- tempo_recorrencia: tempo para recorrência ou censura (em dias);
- censura_recorrencia: variável binária indicando se a paciente teve recorrência (1) ou censura (0).
Nesse caso, deseja-se testar a eficiência do tratamento hormonal para evitar a recorrência do câncer de mama. Dessa forma, a terapia hormonal pode ser vista de maneira análoga à vacina e a recorrência do câncer vista como a infecção pela Covid-19.
1ª Forma de calcular eficácia
Traduzindo a fórmula apresentada para esse cenário tem-se:
- V: número de pacientes que receberam o tratamento hormonal;
- P: número de pacientes que não receberam o tratamento hormonal;
- v: número de pacientes que receberam o tratamento hormonal que tiveram recorrência do câncer;
- p: número de pacientes que não receberam o tratamento hormonal que tiveram recorrência do câncer.
Diante disso, pode-se calcular a eficácia da seguinte forma
V % filter(tratamento_hormonal==1) %>% count() %>% as.numeric()
v % filter(tratamento_hormonal==1,
censura_recorrencia==1) %>% count() %>% as.numeric()
- Número de pessoas que receberam hormônio: 246;
- Número de pessoas que receberam hormônio e tiveram recorrência do câncer: 94.
P % filter(tratamento_hormonal==0) %>% count() %>% as.numeric()
p % filter(tratamento_hormonal==0,
censura_recorrencia==1) %>% count() %>% as.numeric()
- Número de pessoas que receberam hormônio: 440;
- Número de pessoas que receberam hormônio e tiveram recorrência do câncer: 205.
razao_risco <- (v/V)/(p/P) eficacia <- 1-razao_risco
- Razão de risco: 0.82;
- Eficácia: 17.99.
Vale ressaltar que existem muitos outros códigos possíveis para calcular essa eficácia, com o auxílio da função table() por exemplo.
2ª Forma de calcular eficácia: modelo de cox
Para calcular a eficácia utilizando o Modelo Cox, será utilizado o pacote survival.
O ajuste do modelo é feito a partir da função coxph(), e dentro dela é utilizada a função Surv(). Primeiramente, como variável resposta, é passada a função Surv() com a variável de tempo e a variável que informa houve recorrência do câncer ou não. Em seguida, deve-se especificar as covariáveis do modelo, que nesse caso é apenas a variável que determina se a paciente recebeu o tratamento hormonal ou não.
O resultado do modelo ajustado é apresentado abaixo.
library(survival)
modelo_Cox <- coxph(Surv(tempo_recorrencia,censura_recorrencia)~tratamento_hormonal, data=dados)
coefs % data.frame()
ic % data.frame()
Tabela % DT::datatable(rownames = FALSE,
options =
list(language =
list(url = '//cdn.datatables.net/plug-ins/1.10.11/i18n/Portuguese-Brasil.json'),
dom = 't',
columnDefs = list(list(width = '170px', targets = "_all", className = 'dt-center'))
))
| Coeficiente | E.P(Coeficiente) | Exp(Coeficiente) | I.C.(95%) |
|---|---|---|---|
| -0.36 | 0.69 | 0.69 | [0.54;0.89] |
Como é possível notar a partir da saída da função summary(modelo_Cox), os testes de Escore, Razão da Verossimilhança e o de Wald Global foram significativos, com valor-p menor que um nível de significância de 5%. Além disso, a partir do teste individual de Wald para o tratamento hormonal, que nesse caso é similar ao teste global por haver apenas uma variável explicativa, também foi significativo.
A partir do coeficiente estimado -0,3640, é possível obter a razão de risco realizando e − 0,36 = 0,69e − 0,36 = 0,69 como também apresentado na saída do summary. Isso indica que o risco da recorrência do câncer para aquelas pacientes que realizaram o tratamento hormonal é 69,49% do risco apresentado por aquelas que não fizeram o tratamento.
Então, realizando 1 menos essa razão de risco encontrada, obtemos uma eficácia de 30,51%.
razao_risco <- exp(modelo_Cox$coefficients) razao_risco
## tratamento_hormonal ## 0.6948843
eficacia <- 1-razao_risco round(eficacia*100,2)
## tratamento_hormonal ## 30.51
O modelo de Cox para cálculo da eficácia não é só interessante por considerar o tempo, mas também quando são consideradas outras variáveis explicativas como sexo e idade, que podem afetar na eficácia de um tratamento ou vacina.
A estatística é fundamental para as mais diversas áreas que utilizam a ciência para chegar a resultados confiáveis. Aqui no blog falamos muito sobre a estatística nos negócios, mas ela está presente em muitas outras áreas da nossa vida. Talvez mais do que conseguimos perceber.



