Machine learning usando Python

Artigo escrito com a colaboração de Joziani Mota Vieira

Aqui no blog já postamos vários artigos falando sobre machine learning, todos rodados no R, que é a linguagem mais usada aqui na Oper. Hoje resolvemos encarar o desafio de fazer o mesmo trabalho só que usando Python.

Pegamos um banco de dados do kaggle que contém 12 características clínicas para previsão de mortalidade por insuficiência cardíaca e rodamos o seguinte código em Python.

Módulos de Funções no Python

import pandas as pd
import numpy as np
import sklearn as sk
import matplotlib.pyplot as plt
from sklearn import metrics

def plot_corr(df, size=11):
corr = df.corr()
fig, ax = plt.subplots(figsize = (size, size))
ax.matshow(corr)
plt.xticks(range(len(corr.columns)), corr.columns, rotation=90)
plt.yticks(range(len(corr.columns)), corr.columns)

def medidas(mod, predict_test_prob):
predict_test_class = mod.predict(X_teste)
matrix_conf = metrics.confusion_matrix(Y_teste, predict_test_class, labels = [1, 0])
#Acuracia
Acuracia = round(metrics.accuracy_score(Y_teste, predict_test_class),3)
#Sensibilidade/ — TP/(TP + FN)
Sensibilidade = round(matrix_conf[1,1]/(matrix_conf[1,1]+matrix_conf[1,0]),3)
#Especificidade — TN/(TN + FP)
Especificidade = round(matrix_conf[0,0]/(matrix_conf[0,0]+matrix_conf[0,1]),3)
AUC = round(metrics.roc_auc_score(Y_teste, predict_test_prob),3)

return(Acuracia,Sensibilidade,Especificidade, AUC)

Lendo dados no Python

O banco de dados está composto pelas variáveis:

• age = idade
• anaemia = se possui anemia
• creatinine_phosphokinase = nível da enzima CPK no sangue (mcg / L)
• diabetes = se possui diabetes
• ejection_fraction = porcentagem de sangue saindo do coração a cada contração (porcentagem)
• high_blood_pressure = se possui pressão alta
• platelets = plaquetas no sangue (quiloplacas / mL)
• serum_creatinine = nível de creatinina sérica no sangue (mg / dL)
• serum_sodium = nível de sódio sérico no sangue (mEq / L)
• sex = Sexo – 1: masculino e 0: feminino
• smoking = se é fumante
• DEATH_EVENT = se morreu

df = pd.read_csv('dados/heart_failure_clinical_records_dataset.csv', encoding = "latin-1", sep = ';')
df

Análises descritivas

Observamos que não houve dados faltantes. A maior parte dos indivíduos não morreram, não tinham anemia, nem diabetes ou pressão alta. A maioria dos indivíduos foi do sexo masculino e não fumava.

num_vivo = len(df[df['DEATH_EVENT'] == 0])
num_morto = len(df[df['DEATH_EVENT'] == 1])
print('Pessoas que permaneceram vidas: {0} ({1:2.2f}%)'.format(num_vivo, (num_vivo/ (num_vivo + num_morto)) * 100))
print('Pessoas que faleceram: {0} ({1:2.2f}%)'.format(num_morto, (num_morto/ (num_vivo + num_morto)) * 100))

Pessoas que permaneceram vidas: 203 (67.89%)
Pessoas que faleceram: 96 (32.11%)

df.drop(columns=['DEATH_EVENT']).describe()

• a média da idade foi de 60,83, com desvio padrão de 11,89;
• a média do o nível da enzima CPK no sangue foi de 581,84, com desvio padrão de 970,29;
• a média da porcentagem de sangue saindo do coração a cada contração foi de 38,08, com desvio padrão de 11,83;
• a média das plaquetas no sangue foi de 263358,03, com desvio padrão de 97804,24;
• a média do nível de creatinina sérica no sangue foi de 1,39, com desvio padrão de 1,03;
• a média do nível de sódio sérico no sangue foi de 136,63, com desvio padrão de 4,41.

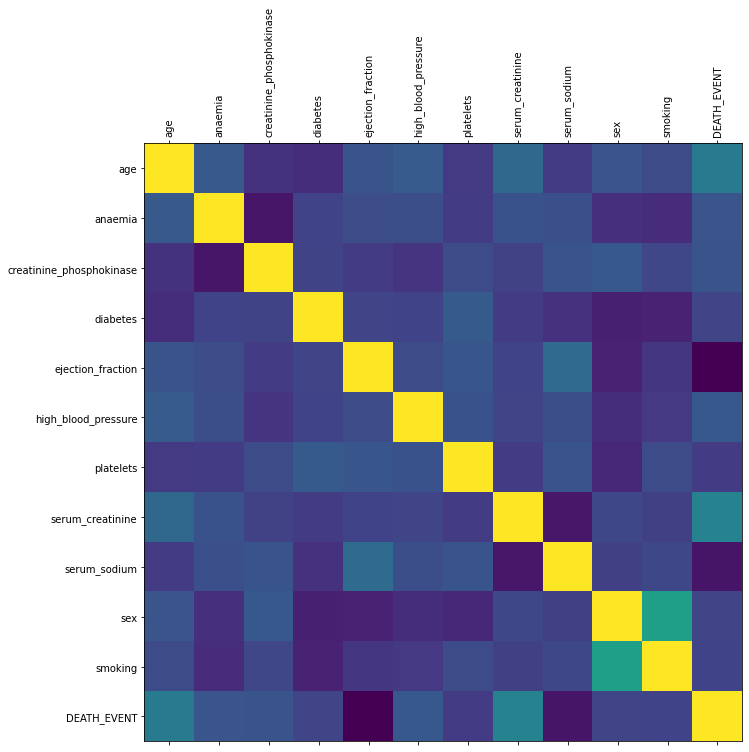
Correlação

Houve correlação positiva e significativa entre se morreu e a variável nível de creatinina sérica no sangue e a variável idade.

Houve correlação negativa e significativa entre se morreu e a variável nível de sódio sérico no sangue e a porcentagem de sangue saindo do coração a cada contração.

df.corr(method = 'spearman')

plot_corr(df)

Método holdout

O método holdout é usado para validação de dados, nele se divide o banco de dados entre treino e teste, sendo que o banco treino é utilizado para treinar os modelos e o banco teste é usado para cálculo de medidas de desempenho dos modelos. Aqui foi usado 70% dos dados para treino e 30% para teste.

Podemos observar que não há preditores com variância zero e nem combinações lineares no banco de dados treino e teste.

from sklearn.model_selection import train_test_split

Criando objetos
X = df.drop(columns=['DEATH_EVENT']).values

Y = df.DEATH_EVENT.values

X_treino, X_teste, Y_treino, Y_teste = train_test_split(X, Y, test_size = 0.30, random_state = 123)
X_treino.shape, X_teste.shape, Y_treino.shape, Y_teste.shape

((209, 11), (90, 11), (209,), (90,))

Regressão logística

from sklearn.linear_model import LogisticRegression

mod_reg1 = LogisticRegression(max_iter = 1000)
mod_reg1 = mod_reg1.fit(X_treino, Y_treino)

predict_reg_prob = mod_reg1.predict_proba(X_teste)
predict_reg_prob = predict_reg_prob[:, 1] # manter somente para a classe positiva

medidas_reg = np.array(medidas(mod_reg1, predict_reg_prob))

print(np.exp(mod_reg1.coef_))

[[1.04935305 1.00277357 1.00014538 0.9993135 0.92424301 1.00240366 0.99999935 1.02104226 0.99283742 0.99792634 0.9962138 ]]

Random forest

from sklearn.ensemble import RandomForestClassifier

mod_rf = RandomForestClassifier(random_state = 123)
mod_rf = mod_rf.fit(X_treino, Y_treino.ravel())

predict_rf_prob = mod_rf.predict_proba(X_teste)
predict_rf_prob = predict_rf_prob[:, 1]

medidas_rf = np.array(medidas(mod_rf, predict_rf_prob))

Support vector machines

from sklearn import svm
from sklearn import calibration

mod_svm = svm.SVC(kernel='linear')
mod_svm = mod_svm.fit(X_treino, Y_treino.ravel())

predict_svm_prob = mod_svm.decision_function(X_teste)
medidas_svm = np.array(medidas(mod_svm, predict_svm_prob))

Medidas

pd.DataFrame({'Regressão' : medidas_reg,'RandomForest': medidas_rf,'SVM' : medidas_svm},
index = ['Acurácia', 'Sensibilidade', 'Especificidade', 'AUC'])

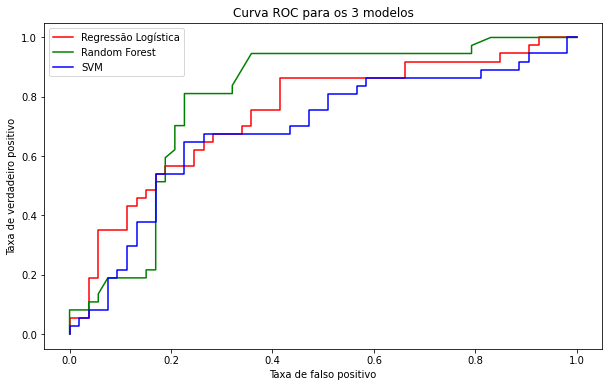
Curva roc

plt.figure(figsize = (10,6))
fpr_reg, tpr_reg, limite1 = metrics.roc_curve(Y_teste, predict_reg_prob)
fpr_rf, tpr_rf, limite2 = metrics.roc_curve(Y_teste, predict_rf_prob)
fpr_svm, tpr_svm, limite3 = metrics.roc_curve(Y_teste, predict_svm_prob)
plt.plot(fpr_reg, tpr_reg, color='red', label='Regressão Logística')
plt.plot(fpr_rf, tpr_rf, color='green', label='Random Forest')
plt.plot(fpr_svm, tpr_svm, color='blue', label='SVM')
plt.xlabel('Taxa de falso positivo')
plt.ylabel('Taxa de verdadeiro positivo')
plt.title('Curva ROC para os 3 modelos')
plt.legend()
plt.show()

Salvando o modelo no Python

import pickle
filename = 'modelos/Modelo Regressão Logística.sav'
pickle.dump(mod_reg1, open(filename, 'wb'))

loaded_model = pickle.load(open(filename, 'rb'))
resultado1 = loaded_model.predict(X_teste[15].reshape(1, -1))
resultado2 = loaded_model.predict(X_teste[18].reshape(1, -1))
print(resultado1)
print(resultado2)

E aí, curtiram esse desafio de trabalhar com Python? Você pode rodar esse código usando o Jupyter notebook online para ver os resultados da análise. Siga a Oper nas redes sociais para ser informado sempre que postarmos novos artigos! Estamos no Instagram, Facebook e Linkedin.