Artigo escrito com a colaboração de Carolina Barcelos
A análise de regressão tem por objetivo desvendar o comportamento entre uma variável dependente (resposta) e as consideradas independentes (explicativas).
Análise de Regressão Simples
A análise de regressão linear simples é responsável por avaliar a relação linear entre duas variáveis, sendo uma resposta e uma explicativa (um preditor). Quando é realizada a comparação das duas variáveis, é possível prever um valor de resposta com uma precisão maior que o simples acaso.
Na regressão linear simples, a relação entre duas variáveis pode ser representada por uma linha reta, criando uma relação direta de causa e efeito. Assim, será possível prever os valores de uma variável dependente com base nos resultados da variável independente.
É estabelecida uma equação
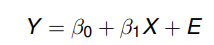
Onde
- Y é a variável dependente (resposta);
- X é a variável independente (explicativa);
- β0 é o intercepto em Y. É o valor esperado de Y quando X = 0;
- β1 é a inclinação (taxa de mudança). É o aumento esperado em Y quando X aumenta uma unidade;
- E é um erro aleatório, onde se procuram incluir todas as influências no comportamento da variável Y que não podem ser explicadas linearmente pelo comportamento da variável X. E ∼ N (0, σ2).
Exemplo
Estamos interessados em saber se o índice de desemprego de um município determina (explica, prediz, interfere no) nível de criminalidade (roubo/furto) do município? Ou seja, se quanto maior os índices de desemprego de um município, maior a taxa de criminalidade.
Análise de Regressão Múltipla
Muitas vezes uma única variável explicativa (preditora) não será capaz de explicar tudo a respeito da variável resposta. Se em vez de uma, forem incorporadas várias variáveis independentes, passa-se a ter uma análise de regressão linear múltipla.
Nesse caso, a equação estabelecida é
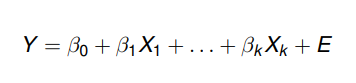
Onde
- Y é a variável dependente (resposta);
- X1, …, Xk são as variáveis independentes (explicativas);
- β0, …, βk são os parâmetros desconhecidos do modelo (a estimar). β0 é o valor esperado de Y quando todas variáveis são iguais a zero. Determinado βj (j diferente de 0) representa a variação no Y quando Xj aumenta em uma unidade (mantendo constantes todos Xi com exceção do Xj). Se βj > 0, Y aumenta e se βj < 0, Y diminui;
- E é um erro aleatório, onde se procuram incluir todas as influências no comportamento da variável Y que não podem ser explicadas linearmente pelo comportamento das variáveis X1, …, Xk. E ∼ N (0, σ2).
Exemplo
Pretendemos determinar se a taxa de criminalidade de um município pode ser medida em função do índice de desemprego e do índice de escolaridade.
Aplicação no R
- Leitura dos pacotes que serão necessários
library(dplyr) #manipulação de dados
library(openxlsx) #leitura dos dados em uma planilha excel
library(corrgram) #correlogramaModelo de Regressão Linear Simples
Para o nosso exemplo de regressão linear simples, usaremos o conjunto de dados “cars”. Ele é composto por 50 observações da velocidade de diferentes carros da década de 20 e da respectiva distância alcançada pelo carros durante o experimento.
dados <- cars
names(dados)## [1] "speed" "dist"- Alterando o nome das variáveis para o português
dados <- dados %>% rename(Velocidade = speed, Distancia = dist)
head(dados)## Velocidade Distancia
## 1 4 2
## 2 4 10
## 3 7 4
## 4 7 22
## 5 8 16
## 6 9 10- Analisando o comportamento dos dados
summary(dados)## Velocidade Distancia
## Min. : 4.0 Min. : 2.00
## 1st Qu.:12.0 1st Qu.: 26.00
## Median :15.0 Median : 36.00
## Mean :15.4 Mean : 42.98
## 3rd Qu.:19.0 3rd Qu.: 56.00
## Max. :25.0 Max. :120.00Se queremos um modelo, é esperado que a variável resposta e a preditora possuam uma boa correlação entre si. Para isso, plotamos os valores de velocidade contra as distâncias:
plot(x = dados$Velocidade,
y = dados$Distancia,
xlab = "Velocidade (mph)",
ylab = "Distancia (ft)",
pch = 16)
O gráfico acima apresenta uma boa relação entre a velocidade do carro e a distância percorrida por eles no experimento.
cor.test(dados$Velocidade, dados$Distancia)##
## Pearson's product-moment correlation
##
## data: dados$Velocidade and dados$Distancia
## t = 9.464, df = 48, p-value = 1.49e-12
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.6816422 0.8862036
## sample estimates:
## cor
## 0.8068949O coeficiente de correlação de pearson concorda com o gráfico, obtendo um valor igual a 0,81.
- Construção do modelo linear
modelo_simples = lm(dados$Distancia ~ dados$Velocidade)
summary(modelo_simples)##
## Call:
## lm(formula = dados$Distancia ~ dados$Velocidade)
##
## Residuals:
## Min 1Q Median 3Q Max
## -29.069 -9.525 -2.272 9.215 43.201
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -17.5791 6.7584 -2.601 0.0123 *
## dados$Velocidade 3.9324 0.4155 9.464 1.49e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.38 on 48 degrees of freedom
## Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
## F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12Com base nas informações acima, podemos afirmar que o modelo é estatisticamente significante (valor-p<0,05), ou seja, a cada aumento em uma unidade na velocidade, espera-se um aumento em 3,93 na distância.
Distância = – 17,58 + 3,93 * Velocidade
O intercepto não tem interpretação prática.
O coeficiente de determinação (R2) foi de 0,6511, indicando que 65,11% da variabilidade dos dados é explicada pelo modelo.
- Verificando a adequação do modelo
Gráfico dos resíduos versus valores ajustados: verifica a homoscedasticidade do modelo, isto é, σ2 constante.
plot(modelo_simples,1) #O ideal é que os pontos estejam distribuídos em torno de uma média 0.
Teste de Breusch-Pagan e Goldfeld-Quandt
H0: os resíduos são homoscedásticos.
H1: os resíduos não são homoscedásticos.
lmtest::bptest(modelo_simples)##
## studentized Breusch-Pagan test
##
## data: modelo_simples
## BP = 3.2149, df = 1, p-value = 0.07297Como o valor-p 0,073 foi maior do que 5% de significância, temos a não rejeição de H0. Assim, a suposição de homocedasticidade foi atendida.
Gráfico dos resíduos versus a ordem de coleta dos dados: avaliar a hipótese de independência dos dados

Teste de Durbin-Watson
H0: os valores dos resíduos do modelo são independentes.
H1: os resíduos são autocorrelacionados.
car::durbinWatsonTest(modelo_simples)## lag Autocorrelation D-W Statistic p-value
## 1 0.1604322 1.676225 0.188
## Alternative hypothesis: rho != 0Como o valor p 0,202 foi maior do que 5% de significância, temos a não rejeição de H0. Assim, a suposição de independência foi atendida.
Papel de probabilidade normal: verificar a normalidade dos dados.
plot(modelo_simples, 2) #O ideal é que os pontos estejam próximos da linha tracejada.
Teste de Shapiro-Wilk
H0: a distribuição Normal modela adequadamente os resíduos do modelo.
H1: a distribuição Normal não modela adequadamente os resíduos do modelo.
shapiro.test(modelo_simples$residuals)##
## Shapiro-Wilk normality test
##
## data: modelo_simples$residuals
## W = 0.94509, p-value = 0.02152Como o valor-p 0,022 foi menor do que 5% de significância, temos a rejeição de H0. Assim, a suposição de normalidade não foi atendida.
Nesse caso, temos que os erros padrões não estão corretos, o que implica em valores-p incorretos. Uma possível solução para isso seria utilizar erros padrões robustos, mas se o interesse for apenas nas estimativas, por exemplo, o modelo está adequado para uso, uma vez que a condição de homocedasticidade e independência foram atendidas.
Vale ressaltar que se existe normalidade, automaticamente existe homocedasticidade, mas o contrário não é válido!
Modelo de Regressão Linear Múltipla
Para o nosso exemplo de regressão linear múltipla, usaremos uma amostra aleatória do conjunto de dados da TRAVEL, uma empresa de transporte independente no sul da Califórnia, onde grande parte dos negócios envolve entregas em toda a sua área local.
O banco de dados é composto por 10 observações referentes à distância (número de milhas percorridas nas entregas), ao número de entregas e ao tempo total de viagem diário (em horas) de diferentes entregadores da empresa.
df <- read.xlsx("dados_multipla.xlsx", startRow = 1)
df## Entregador Distancia Entregas Tempo
## 1 1 100 4 9.3
## 2 2 50 3 4.8
## 3 3 100 4 8.9
## 4 4 100 2 6.5
## 5 5 50 2 4.2
## 6 6 80 2 6.2
## 7 7 75 3 7.4
## 8 8 65 4 6.0
## 9 9 90 3 7.6
## 10 10 90 2 6.1- Analisando o comportamento dos dados
summary(df)## Entregador Distancia Entregas Tempo
## Min. : 1.00 Min. : 50.0 Min. :2.00 Min. :4.200
## 1st Qu.: 3.25 1st Qu.: 67.5 1st Qu.:2.00 1st Qu.:6.025
## Median : 5.50 Median : 85.0 Median :3.00 Median :6.350
## Mean : 5.50 Mean : 80.0 Mean :2.90 Mean :6.700
## 3rd Qu.: 7.75 3rd Qu.: 97.5 3rd Qu.:3.75 3rd Qu.:7.550
## Max. :10.00 Max. :100.0 Max. :4.00 Max. :9.300Se queremos um modelo, é esperado que a variável resposta e as preditoras possuam uma boa correlação entre si. Para isso, plotamos um correlograma das variáveis de interesse:
x <- df[,-1] #excluindo a coluna "Entregador"
corrgram(x,
#upper.panel=panel.cor,
upper.panel=panel.conf,
cex.labels=1.5, cex=1.2)
O gráfico acima apresenta uma boa relação entre o tempo e a distância (r = 0,81), bem como entre o tempo e o número de entregas (r = 0,62).
- Construção do modelo linear
modelo_multipla = lm(Tempo ~ Distancia + Entregas, data = df)
summary(modelo_multipla)##
## Call:
## lm(formula = Tempo ~ Distancia + Entregas, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.79875 -0.32477 0.06333 0.29739 0.91333
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.868701 0.951548 -0.913 0.391634
## Distancia 0.061135 0.009888 6.182 0.000453 ***
## Entregas 0.923425 0.221113 4.176 0.004157 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.5731 on 7 degrees of freedom
## Multiple R-squared: 0.9038, Adjusted R-squared: 0.8763
## F-statistic: 32.88 on 2 and 7 DF, p-value: 0.0002762Com base nas informações acima, podemos afirmar que tanto a distância, quanto o número de entregas são estatisticamente significantes no modelo (valor-p<0,05).
Quando o número de entregas é mantido constante, 0,06 horas é uma estimativa do aumento esperado no tempo de viagem, quando ha um aumento de uma milha na distância percorrida.
Da mesma forma, quando a distância é mantida constante, 0,92 horas é uma estimativa do aumento esperado no tempo de viagem, quando ha um aumento de uma entrega.
Tempo = – 0,87 + 0,06 * Distância + 0,92 * Entregas
O intercepto não tem interpretação prática.
O coeficiente de determinação ajustado (R2 ajustado) foi de 0,8763, indicando que 87,63% da variabilidade dos dados é explicada pelo modelo. Ressalta-se que para modelos de regressão que contêm diferentes números de preditores, utiliza-se o coeficiente de determinação ajustado, que é uma versão modificada do coeficiente de determinação, que foi ajustada para o número de preditores no modelo. O R2 ajustado aumenta somente se o novo termo melhorar o modelo mais do que seria esperado pelo acaso. Ele diminui quando um preditor melhora o modelo menos do que o esperado por acaso. O R2 ajustado é sempre menor que o R2.
- Verificando a adequação do modelo
Gráfico dos resíduos versus valores ajustados: verifica a homoscedasticidade do modelo, isto é, σ2 constante.
plot(modelo_multipla,1) #O ideal é que os pontos estejam distribuídos em torno de uma média 0.
Teste de Breusch-Pagan e Goldfeld-Quandt
H0: os resíduos são homoscedásticos.
H1: os resíduos não são homoscedásticos.
lmtest::bptest(modelo_multipla)##
## studentized Breusch-Pagan test
##
## data: modelo_multipla
## BP = 0.36899, df = 2, p-value = 0.8315Como o valor-p 0,832 foi maior do que 5% de significância, temos a não rejeição de H0. Assim, a suposição de homocedasticidade foi atendida.
Gráfico dos resíduos versus a ordem de coleta dos dados: avaliar a hipótese de independência dos dados
plot(modelo_multipla$residuals) #espera-se que os pontos estejam distribuídos de forma aleatória.
Teste de Durbin-Watson
H0: os valores dos resíduos do modelo são independentes.
H1: os resíduos são autocorrelacionados.
car::durbinWatsonTest(modelo_multipla)## lag Autocorrelation D-W Statistic p-value
## 1 -0.317467 2.515204 0.392
## Alternative hypothesis: rho != 0Como o valor p 0,39 foi maior do que 5% de significância, temos a não rejeição de H0. Assim, a suposição de independência foi atendida.
Papel de probabilidade normal: verificar a normalidade dos dados.
plot(modelo_multipla, 2) #O ideal é que os pontos estejam próximos da linha tracejada.
Teste de Shapiro-Wilk
H0: a distribuição Normal modela adequadamente os resíduos do modelo.
H1: a distribuição Normal não modela adequadamente os resíduos do modelo.
shapiro.test(modelo_multipla$residuals)##
## Shapiro-Wilk normality test
##
## data: modelo_multipla$residuals
## W = 0.97848, p-value = 0.9565Como o valor-p 0,957 foi maior do que 5% de significância, temos a não rejeição de H0. Assim, a suposição de normalidade foi atendida.
Curiosidade
A Regressão Linear é uma das técnicas mais utilizadas em Aprendizagem de Máquina!
Curtiu o nosso conteúdo? Siga-nos nas redes sociais para ficar por dentro de toda as novidades do blog! Estamos no Linkedin, Instagram e Facebook.



