Uma das grandes contribuições da estatística para ampliar o entendimento humano sobre os fenômenos observados é a capacidade de medir a relação entre diferentes variáveis. Os coeficientes de correlação auxiliam os pesquisadores a mensurar essa relação.
Pensando nisso, elaboramos este artigo para mostrar os principais coeficientes de correlação e quando cada um deles deve ser utilizado.
O que são coeficientes de correlação?
Os coeficientes de correlação são métodos estatísticos para se medir as relações entre variáveis e o que elas representam.
O que a correlação procura entender é como uma variável se comporta em um cenário onde outra está variando, visando identificar se existe alguma relação entre a variabilidade de ambas. Embora não implique em causalidade, o coeficiente de correlação exprime em números essa relação, ou seja, quantifica a relação entre as variáveis.
Em pesquisas científicas os coeficientes de correlação são muito importantes para se traçar panoramas em estudos com muitas variáveis relacionadas, pois assim é possível entender como a variabilidade de uma afeta a outra.
Mas não existe apenas uma forma de se calcular a correlação entre variáveis. Dependendo da forma e de como se comportam as variáveis, um coeficiente de correlação é mais adequado que outro.
Coeficiente de Correlação de Pearson
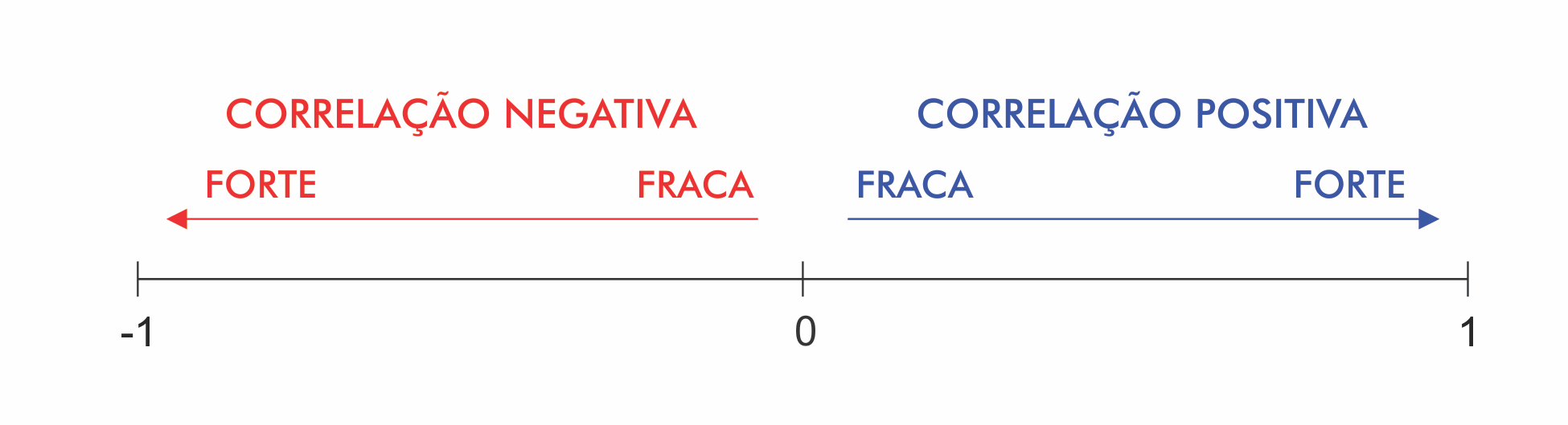
O coeficiente de correlação de Pearson (r), também chamado de correlação linear ou r de Pearson, é um grau de relação entre duas variáveis quantitativas e exprime o grau de correlação através de valores situados entre -1 e 1.
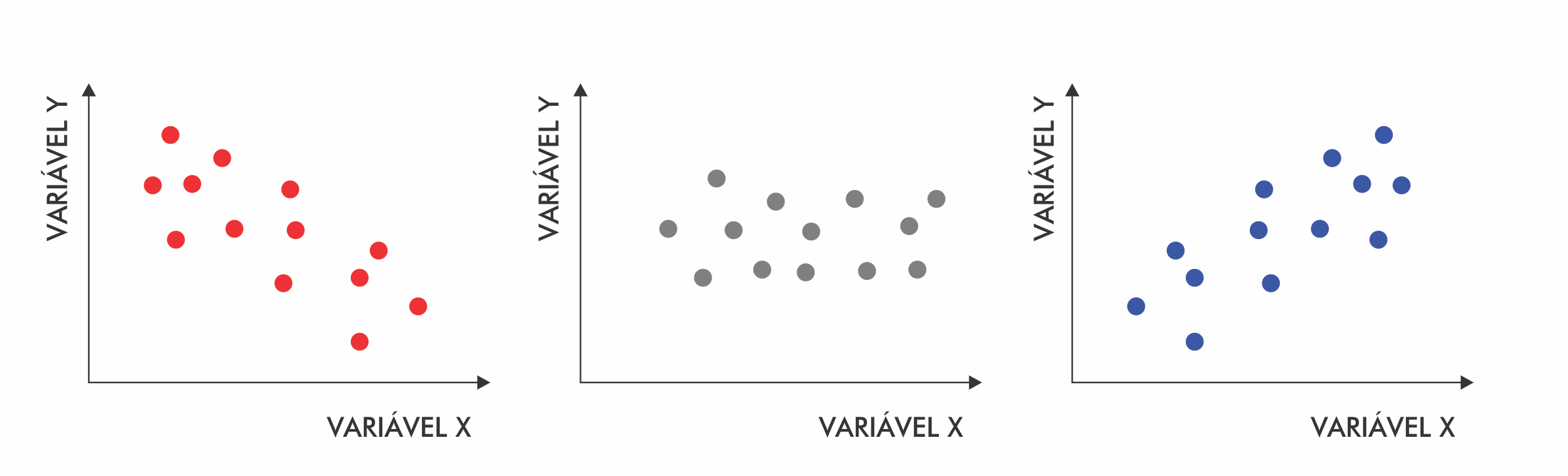
Quando o coeficiente de correlação se aproxima de 1, nota-se um aumento no valor de uma variável quando a outra também aumenta, ou seja, há uma relação linear positiva. Quando o coeficiente se aproxima de -1, também é possível dizer que as variáveis são correlacionadas, mas nesse caso quando o valor de uma variável aumenta o da outra diminui. Isso é o que é chamado de correlação negativa ou inversa.
Um coeficiente de correlação próximo de zero indica que não há relação entre as duas variáveis, e quanto mais eles se aproximam de 1 ou -1, mais forte é a relação.
Coeficiente de Correlação de Spearman
Denominado pela letra grega rho (ρ), o coeficiente de correlação de postos de Spearman é uma medida de correlação não paramétrica também avaliado no intervalo entre -1 e 1.
Ao contrário do coeficiente de Pearson, o coeficiente de Spearman não exige a suposição de que a relação entre as variáveis seja linear, nem requer que as mesmas sejam quantitativas – pode inclusive ser utilizado para verificar relação entre variáveis medidas no nível ordinal.
Coeficiente de Correlação de Kendall
Expresso pela letra grega tau (τ), o coeficiente de correlação de Kendall é uma medida de associação para variáveis ordinais. Uma vantagem de tau sobre o coeficiente de Spearman é a possibilidade de ser generalizado para um coeficiente de correlação parcial.
Aplicação dos coeficientes de correlação: tempo de estudo X notas nas provas
Pensemos em uma situação hipotética. Um professor percebe que alguns de seus alunos não estão apresentando bom desempenho nas provas e, percebendo que estes não estavam dedicando tempo suficiente aos estudos, decide fazer uma pequena experiência com a turma.
Ele então pede que os alunos informem o tempo que cada um dedicou em casa ao estudo do conteúdo cobrado e monta a seguinte tabela:
| Aluno | Horas de Estudo | Nota |
| 1 | 20 | 9,5 |
| 2 | 12 | 2,5 |
| 3 | 14 | 3,6 |
| 4 | 15 | 6,7 |
| 5 | 18 | 5,2 |
| 6 | 9 | 1 |
| 7 | 5 | 0 |
| 8 | 4 | 1,5 |
| 9 | 8 | 2 |
| 10 | 13 | 3 |
| 11 | 14 | 3,5 |
| 12 | 15 | 4,5 |
| 13 | 19 | 8,5 |
| 14 | 18 | 7,5 |
| 15 | 12 | 5 |
| 16 | 11 | 4 |
| 17 | 10 | 3 |
| 18 | 15 | 5 |
| 19 | 17 | 6,5 |
| 20 | 20 | 10 |
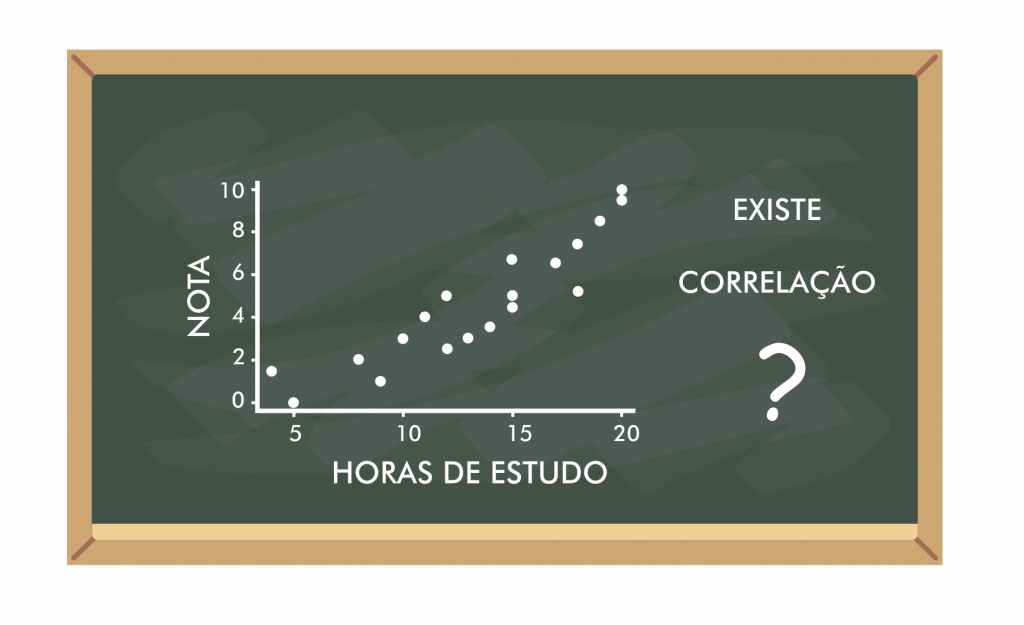
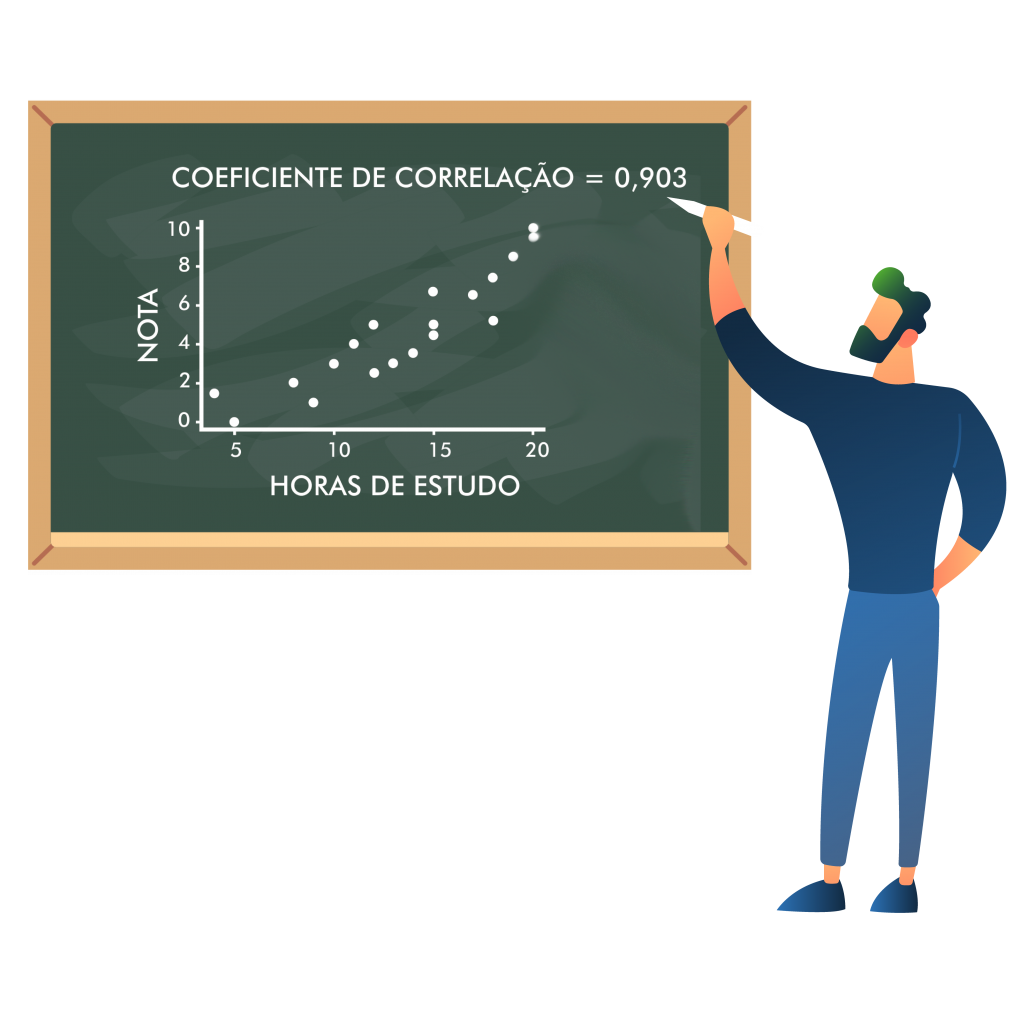
Ele explica aos alunos que se existe uma relação entre as horas de estudo com as notas da prova, isso poderia facilmente ser observado em um gráfico. Utilizando o eixo X para as horas de estudo e o eixo Y para a nota na prova, marca no gráfico a nota e o tempo de estudo de cada aluno.
Coeficientes de correlação: quantificando a relação entre variáveis
Visualmente parece haver alguma relação do tempo de estudo e a nota da prova, pois quanto maior o tempo de estudo, maior tende a ser a nota do aluno. Mas como confirmar e quantificar essa relação?
Além de calcular o coeficiente de correlação, existem testes estatísticos que permitem avaliar as hipóteses de que o coeficiente é igual a zero (hipótese nula) e de que ele é diferente de zero (hipótese alternativa).
O professor então decide utilizar o coeficiente de correlação de Pearson e chegou ao valor de r = 0,903, com p-valor de 0,000.
Interpretando os resultados do coeficiente de correlação
Ora, se o coeficiente de correlação de Pearson sustenta resultados entre -1 e 1, sendo que quanto mais próximo de -1, maior a correlação negativa entre as variáveis, e quanto mais próximo de 1, maior a correlação positiva, podemos dizer que nesse caso existe uma relação positiva entre horas de estudo e a nota da prova, como era de se esperar.
Além disso, o p-valor do teste de Pearson de 0,000 indica a rejeição da hipótese de que o coeficiente de correlação seja igual a zero, indicando que existe uma relação significativa entre as variáveis testadas.
Após apresentar evidências de que quanto mais um aluno estude em casa, maior tende a ser sua nota na prova, o professor espera que os alunos se dediquem mais aos estudos!
Correlação significativa implica em relação de causalidade?
Os coeficientes de correlação podem ser utilizados para identificar e medir a relação presentes em variáveis de nosso cotidiano, como a taxa de desemprego e o índice de criminalidade, a poluição no ar com problemas respiratórios, etc.
Os coeficientes de correlação são muito importantes na evolução do conhecimento humano e muito dos avanços científicos que tanto beneficiam nossas vidas, utilizaram desse conceito em seu desenvolvimento. Mas será que o fato de duas variáveis estarem correlacionadas, essa relação implica em causalidade? Ou seja, uma correlação significativa implica em uma relação de causa e efeito entre as variáveis? A resposta é NÃO.
Abordaremos causalidade e correlação em nossos futuros artigos. Então não deixe de acompanhar o nosso Blog. Caso tenha alguma dúvida sobre os coeficientes de correlação, não deixe de entrar em contato com nossos Data Talkers.




25 comentários em “Coeficientes de Correlação”
ótimo conteúdo, exatamente o que eu precisava
Excelente explicação___Ajudou a interpretar rapidamente coeficiente de Pearson__utilizado em artigo cientifico sobre crianças graves internadas em Uti Pediátrica em Milão Itália__ A relação verificada foi instabilidade clinica e aumento de volume de infusão diária de soluções intravenosas.
Valeu !!!__continuem assim fornecendo conteúdos gratuitos___para quem gosta de estudar__
PS__como sou Professor de Medicina __aprendi mais e adorei a explicação que associa notas de alunos e tempo de estudo_–Parabéns__ para isso serve a ciência__e a estatística__
Aconselho leitura de” Guidelines”_ britânico sobre ética em estatística _para todos que lidam com conteúdos digitais… Abçs__JC.__FAMED/UFMS
Muito obrigada, João Cândido. Bom saber que o artigo te ajudou!
Esse blog é bom mesmo. Parabéns.
Que bom que você curtiu!
Muito bom e didático, não tem como não entender! fora que é tudo muito bem pensado e ilustrado.
Melhor site sobre assuntos de estatística! Extremamente didático!
Valeu, Natan!
Sou novo na matéria,como Chegou no coeficiente = ,9..?
Oi Felício, o valor r = 0,903 foi obtido através do coeficiente de correlação de Pearson. O artigo não teve como foco apresentar o aspecto algébrico do cálculo feito, porém, para reproduzir o exemplo de maneira simples, basta aplicar a função PEARSON do Excel sobre as colunas de interesse.
Ótima explicação! Parabéns! me ajudou bastante a compreender melhor sobre análises que irei utilizar em minha pesquisa do mestrado.
Obrigada, Daiane! Boa sorte no mestrado!
Pingback: Fazendo previsão com Machine Learning – Espaço Diegeux
Parabéns pelo conteúdo! Ajudou a entender melhor a correlação.
Fiquei com uma dúvida: vemos que os alunos com mais tempo de estudo tiveram notas maiores. Isso também seria causalidade?
Visto que o evento A (horas de estudos) influenciou o evento B (notas das provas).
Muito boa sua pergunta André! Não, o fato de uma variável apresentar correlação significativa com outra variável não implica em relação de causa e efeito entre elas.
Adorei o artigo. Aproveitando a questão do André. Há alguma técnica ou método capaz de me dizer se há ou não causalidade entre variáveis com correlação significativa?
Sim, há algumas técnicas e métodos que podem ajudar a determinar a causalidade entre variáveis com correlação significativa. No entanto, é importante notar que a correlação não implica necessariamente causalidade.
Uma abordagem comum é usar técnicas de modelagem causal, como a análise de causalidade de Granger e modelos VAR (vetores autorregressivos). Essas técnicas usam uma série de dados históricos para determinar se as mudanças em uma variável antecedem as mudanças em outra variável.
Outra abordagem é realizar experimentos controlados para determinar a causalidade. Nesses casos, uma variável é manipulada enquanto outras variáveis são mantidas constantes para ver se há um efeito causal.
No entanto, é importante lembrar que a determinação da causalidade requer mais do que apenas uma correlação significativa entre as variáveis. É importante levar em conta outras informações contextuais relevantes e estar ciente das limitações do método escolhido.
Adilane adorei as explicações sobre o caso R de Pearson, estava com muitas dúvidas em psicometria este conteúdo clareou bastante minhas dúvidas. Obrigado
Valeu Luiz! Que bom que conseguiu resolver as dúvidas.
Bom dia,
Tenho duas variáveis uma chamada caso de Doença de Chagas e outra chamada desmatamento, quem é a variável depende e independente? Gostaria de aplicar o teste de correlação de Pearson.
Cordialmente,
Clístenes Catete
Oi Clístenes! Com o desmatamento, há um aumento de barbeiros, e consequentemente, o número de casos de doença de chagas evolui. Porém é preciso ter um conhecimento prévio para definir as variáveis, pois o aumento do desmatamento pode influenciar nos casos de doenças de chagas, enquanto é mais improvável que o aumento dos casos de doenças de chagas influenciem no desmatamento. Portanto os “casos de chagas” seria a variável dependente.
Excelente explicação! Obrigado.
Obrigada, Josielson!
Boa tarde!
Coeficientes de correlação servem, então, para realizar associação entre dois fenômenos (que seriam as variáveis)?
Obrigada.
Oi, Cristiane! Não para realizar associação, mas sim para medir o grau de associação entre duas variáveis de escala métrica (numérica). Tendo valores entre -1 e 1.