Em estudos que buscam comparar a distribuição de três ou mais grupos de amostras independentes, frequentemente se utiliza a Análise de Variância ou ANOVA. Nesse caso, o resultado evidencia que a distribuição de pelo menos um dos grupos se difere das demais, mas não indica entre quais grupos a diferença é significativa. Assim, se faz necessário utilizar testes de comparações múltiplas e hoje, abordaremos um deles: o Teste de Tukey.
Para ilustrar a aplicação e utilização do Teste de Tukey, continuaremos utilizando o exemplo fictício apresentado no artigo sobre “Como interpretar uma Análise de Variância”. Nele, se buscava verificar se o desempenho na prova de matemática de alunos de um curso preparatório para o ENEM variava de acordo com o professor que lecionava a disciplina.
No exemplo, os resultados indicaram que existia pelo menos dois professores com alunos com desempenho significativamente diferentes. Agora, utilizaremos o Teste de Tukey para verificar quais são eles.
Leia também: Como interpretar uma Análise de Variância (ANOVA)
O Teste de Tukey
Dentre os testes de comparações múltiplas mais utilizados, o Teste de Tukey se destaca por ser poderoso ao fazer comparações entre todos os pares e também por ser de fácil aplicação. Também é conhecido como Teste de Tukey HSD (Teste de Tukey da Diferença Honestamente Significativa).
O teste de Tukey foi desenvolvido por John Wilder Tukey e apresentado em 1949 no artigo titulado “Comparing Individual Means in the Analysis of Variance” (Biometrics. 5 (2): 99–114. JSTOR 3001913).

Quando os tamanhos amostrais dos grupos são iguais, o Teste de Tukey é um teste exato, ou seja, para o conjunto de todas as comparações par a par, a taxa de erro do conjunto dos testes é exatamente α (nível de significância) e o intervalo de confiança é também exatamente 1 – α. Vale ressaltar que testes de comparações múltiplas exatos são raros, uma vez que a maioria não controla o nível de significância adotado.
O Teste de Tukey consiste em comparar todos os possíveis pares de médias e se baseia na diferença mínima significativa (D.M.S.), considerando os percentis do grupo. No cálculo da D.M.S. utiliza-se também a distribuição da amplitude estudentizada, o quadrado médio dos resíduos da ANOVA e o tamanho amostral dos grupos.
Mas, e quando os tamanhos amostrais dos grupos são diferentes? Devo usar outro teste de comparação múltipla?
Quando os tamanhos amostrais dos grupos são diferentes, o Teste de Tukey ainda pode ser usado. Apesar de não ser mais um teste exato, é um teste aproximado. Nesse caso, o Teste de Tukey é alterado e passa a ser chamado de Tukey-Kramer, que também considera em sua metodologia o tamanho amostral de cada grupo.
Aplicação do Teste de Tukey
No artigo sobre a interpretação da ANOVA, verificamos que existia uma diferença significativa no desempenho dos grupos de alunos de cada professor. Mas será que apenas o grupo de alunos de um professor se difere dos demais? Ou todos se diferem entre si? Observe que neste caso existem três comparações par a par a serem realizadas.
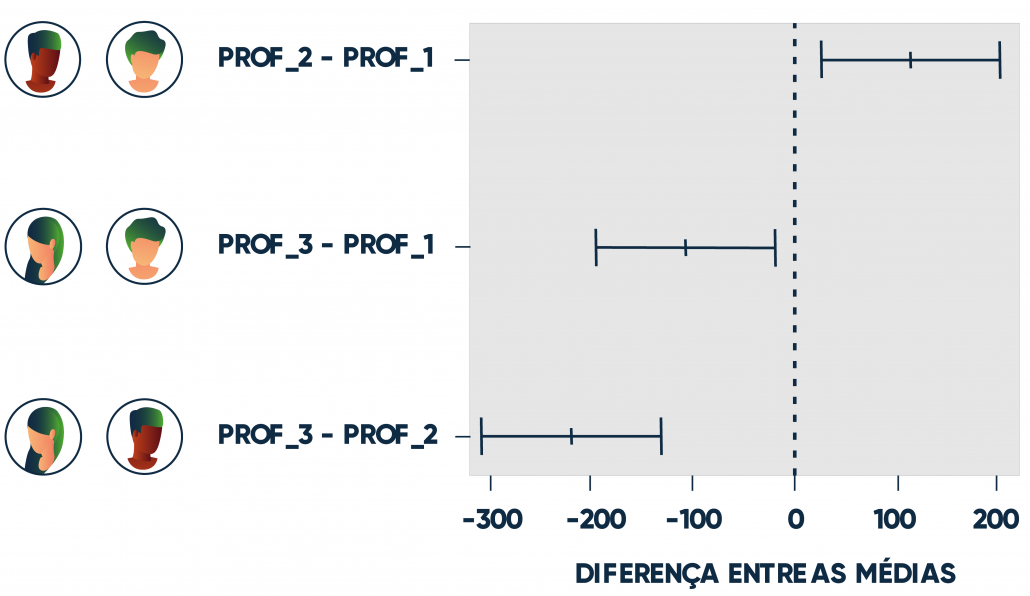
Os resultados obtidos do Teste de Tukey são apresentados na tabela abaixo, que mostra a diferença mínima significativa, a diferença entre as médias do desempenho do grupo de alunos de cada professor, o intervalo de confiança e o valor-p.
| Diferença Mínima Significativa | Professores | Diferença | I.C – 95% | Valor P |
| 88,18 | PROF_2 – PROF_1 | 113,75 | [25,57 ; 201,93] | 0,009 |
| PROF_3 – PROF_1 | -107,08 | [-195,27 ; -18,90] | 0,014 | |
| PROF_3 – PROF_2 | -220,83 | [-309,02 ; -132,65] | 0,001 |
Como interpretar os resultados do Teste de Tukey?
O teste pode ser interpretado com base no valor da diferença mínima significativa (D.M.S.), no intervalo de confiança e no valor-p.
- Diferença Mínima Significativa – Em nosso exemplo, observamos que o módulo da diferença da média entre os pares de professores foi maior que o valor da D.M.S. obtido. Isso nos leva a concluir que o desempenho médio dos alunos dos professores (1 e 2), (1 e 3) e (2 e 3) são significativamente diferentes.
- Intervalo de Confiança – Notamos que o valor 0 (zero) não está contido nos intervalos de confiança. A partir disso, conclui-se também que o desempenho médio dos alunos dos professores (1 e 2), (1 e 3) e (2 e 3) são significativamente diferentes.
- Valor P – Considerando o valor-p, notamos que todos eles são menores que o nível de significância adotado (valor-p < 0,05). Dessa maneira, chegamos a mesma conclusão baseada na D.M.S e nos intervalos de confiança.
Como realizar o Teste?
No software R há pelo menos duas maneiras de realizar o Teste de Tukey: através do função TukeyHSD, ou função HSD.test do pacote agricolae. O resultado obtido em ambos os casos é o mesmo, porém em um dos comandos obtém-se o valor do D.M.S, enquanto que no outro tem-se o intervalo de confiança e o valor-p.
Pressupostos para utilização do teste
Para realizar o Teste de Tukey, deve ser levada em conta as seguintes suposições:
- As observações são independentes dentro e entre os grupos;
- Os grupos devem ser normalmente distribuídos;
- A variância dentro do grupo deve ser constante.
Mas o que fazer quando a suposição da normalidade, por exemplo, não é atendida?
Um procedimento alternativo à ANOVA e ao Teste de Tukey é o teste de Kruskal-Wallis e o teste de comparação múltipla de Nemenyi, temas que serão abordados em futuros artigos. Por isso, não deixe de acompanhar nosso Blog.




3 comentários em “Teste de Tukey para Comparações Múltiplas”
Gosto muito da sua forma de apresentar o teste, mas creio que existe uma confusão na configuração da sua tabela de resultados. Os valores estão confundindo o entendimento de quem não conhece o teste.
No mais parabéns!
Boa tarde!
Queria conhecer sobre o teste de Tukey-Kramer para fazer comparativo entre grupos com tamanho de amostras diferentes. Você tem algum post a respeito ou indica algum material? Obrigada!
Bom dia, Viviane!
Ainda não temos um artigo que fale diretamente sobre Tukey-Kramer, mas podemos indicar esse aqui: http://soniavieira.blogspot.com/2017/01/teste-de-tukey-kramer.html. Se sua dúvida persistir, avisa pra gente!