Artigo escrito com a colaboração de Bruna Faria
A Análise de Variância ou ANOVA é um procedimento usado para comparar a distribuição de três ou mais grupos em amostras independentes.
A análise de variância é também uma forma de resumir um modelo de regressão linear através da decomposição da soma dos quadrados para cada fonte de variação no modelo e, utilizando o teste F, testar a hipótese de que qualquer fonte de variação no modelo é igual a zero.
Contextualizando uma aplicação da Anova
Suponha um curso preparatório para o ENEM que tenha em seu corpo docente três professores de matemática, que são responsáveis por diferentes turmas de alunos. A direção da escola suspeita que a variação do desempenho dos alunos nas provas de matemática do ENEM pode ser explicada pelo trabalho desenvolvido pelos seus professores.
Sendo assim, a direção resolveu verificar as notas na prova de matemática dos alunos de cada professor e calculou a média das notas de cada turma.

Mas será que essa informação é suficiente para afirmar que o desempenho dos alunos de cada turma é realmente diferente? E se um dos professores tiver em sua turma um aluno que não se preparou e errou quase todas as questões? Esse aluno não seria responsável por ter diminuído a média do grupo de alunos desse professor?
Para verificar então se realmente o desempenho dos alunos variou de acordo com o professor, é necessário a utilização de teste estatístico, que além de considerar a média das notas, leva também em conta a variação das notas dentro de cada turma.
A Análise de Variância
Um dos objetivos da aplicação da ANOVA é realizar o teste estatístico para verificar se há diferença entre distribuição de uma medida entre três ou mais grupos. Em nosso exemplo, podemos definir as hipóteses do teste como:
- H0: Não existe diferença entre o desempenho das notas dos alunos de cada professor.
- H1: Há pelo menos um professor com alunos com desempenho diferente.
Mas o que significa diferença entre as distribuições? Qual a relação entre as distribuições das notas dos alunos de cada professor e as hipóteses testadas pela análise de variância?
Caso os três grupos de alunos apresentem mesma variabilidade e a mesma média de desempenho, suas distribuições tendem a se sobrepor, confirmando a hipótese de que não existe diferença entre o desempenho das notas dos alunos de cada professor. Caso contrário, quando os grupos apresentam a mesma variabilidade interna e médias de desempenho diferentes, as distribuições se distanciam quanto mais as médias de desempenho se diferenciam.
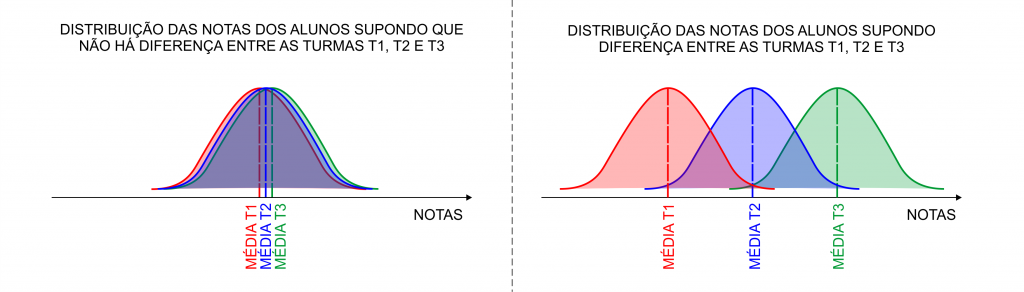
O modelo ANOVA e seus pressupostos
Para aplicação da análise de variância, são necessárias algumas suposições, sendo elas:
- As observações são independentes, ou seja, cada elemento amostral (aluno) deve ser independente;
- Os grupos comparados apresentam a mesma variância;
- Os erros são independentes e provenientes de uma distribuição normal com média igual a zero e variância constante.
Cabe ressaltar que os grupos de alunos de cada professor podem ser vistos como três níveis de um mesmo fator, sendo que o objetivo é saber se o fator professor exerce alguma influência na variação do desempenho das notas de matemática.
Quais são os resultados gerados pela análise de variância?
As informações geradas na análise de variância estão resumidas na tabela abaixo. Nela são apresentados os graus de liberdade, a soma de quadrados, o quadrado médio, a estatística F e o valor-p.
| Fonte de Variação | Graus de Liberdade | Soma de Quadrados | Quadrado Médio | Estatística F | Valor P |
|---|---|---|---|---|---|
| Tratamentos | 2 | 56.806 | 28.403 | 5,25 | 0,010 |
| Resíduos | 33 | 178.783 | 5.418 | ||
| Total | 35 | 235.589 | – |
Os graus de liberdade são calculados com base no número de professores (grupos) e no número total de alunos.
A soma de quadrados mede a variação dos dados. A soma de quadrados total mede a variação total nos dados, a soma de quadrados dos tratamentos mede a variação entre os professores de cada turma e a soma dos quadrados dos resíduos mede a variação dentro de cada turma, ou seja, mede a variação dos alunos de cada professor.
O quadrado médio é a razão entre a soma de quadrados e os graus de liberdade e a estatística F, pode ser encontrada na tabela de distribuição F de Fisher- Snedecor.
Como interpretar os resultados da ANOVA?
Tomando como base a tabela anterior, pode-se concluir que existe pelo menos dois professores com alunos com desempenho significativamente diferentes ao avaliar o valor-p = 0,010 (menor que o nível de significância estabelecido de 0,05).
A conclusão da ANOVA pode ser feita também com base na Estatística F. A estatística F tem distribuição F de Fisher-Snedecor com k-1 e n-k graus de liberdade, onde k é o número de grupos (k = 3) e n é o número de observações (n = 36). Neste caso fictício, obteríamos F ≅ 3,32 e como a Estatística F (5,25) foi maior que o F tabelado (3,32), conclui-se que existe pelo menos dois professores com alunos com desempenho significativamente diferentes.
Mas como saber quais professores com alunos com desempenhos diferentes diferem entre si? A forma de averiguar isto é complementar a ANOVA, através da utilização do teste de comparação múltipla, como por exemplo, o teste de Tukey (veja aqui nosso artigo sobre o teste).
Se interessou por Análise de Variância e os resultados obtidos ao utilizar esta técnica? Não deixe de se registrar em nosso Blog, para acompanhar nossas publicações e caso tenha alguma dúvida, entre em contato com nossos Data Talkers.




29 comentários em “Como interpretar uma Análise de Variância (ANOVA)?”
Caraca, que explicação foda! Muito obrigada!
Valeu Ana, ficamos felizes que você tenha gostado!
Massa, melhor explicação. Estou trabalhando agora com as dicas que deu!
Valeu Ana, ficamos felizes com o feedback! 😀
Excelente explicação! Fácil de entender.
Valeu Sabrina! 🙂
Muito boa a explicação! Só fiquei em dúvida no cálculo da soma de quadrados, não compreendi como chegou no valor exemplo da tabela…
Valeu, Taisa! Para a soma dos quadrados do tratamento pegamos a média da nota da sala 1, subtraímos da média geral de todas as salas e elevamos isso ao quadrado. Fazemos o mesmo para todas as salas e somamos tudo isso. Para a soma dos quadrados dos resíduos pegamos a nota do indivíduo 1 da sala 1, subtraímos da média da nota da sala e elevamos ao quadrado. Fazemos o mesmo para todos os alunos de todas as salas e somamos tudo. E, por último, a soma dos quadrados totais é igual à soma dos quadrados dos tratamentos mais a soma dos quadrados dos resíduos.
Excelente conteúdo sobre teste estatístico ANOVA. Valeu.
Valeu, Walter!
como posso referenciar estas informações?
Oi Kevyn, de acordo com a ABNT você pode referenciar esse artigo assim: OLIVEIRA, Bruno. Como Interpretar Uma Análise De Variância (Anova)?. 2019. Disponível em: . Acesso em: 25 jan. 2021.
Oi pessoal! Muito didática a explicação. Mas se por acaso eu verificar que não há igualdade de variâncias? Posso prosseguir assim mesmo com a Anova? Quais as implicações nesse caso? Obrigado.
Se as variâncias não forem iguais, é melhor utilizar outro teste, como o não-paramétrico Kruskall-Wallis (leia aqui https://operdata.com.br/blog/teste-de-kruskal-wallis-e-o-teste-de-nemenyi/). Quanto mais diferentes forem as variâncias, mais o p-valor da ANOVA estará incorreto, uma vez que o método exige esse pressuposto.
Como é feito o cálculo da estatística F e do valor-p?
A estatística F é uma razão de duas variâncias. As variâncias são uma medida de dispersão e medem o quanto os dados estão dispersos em relação à sua média. Valores maiores representam maior dispersão. Já o p-valor é calculado usando a distribuição amostral da estatística de teste sob a hipótese nula. Ou seja, após aplicação de um teste, o p-valor é o que valida, ou não, a hipótese inicial levantada. Um valor-p pequeno significa que a probabilidade de obter um valor da estatística de teste como o observado é muito improvável, levando assim à rejeição da hipótese nula.
Oi ADILANE, gostei do conteudo esta excelente, obrigado.
O quadrado médio corresponde a decomposição da variância?
Ou seria apenas a média da soma dos quadrados?
Olá, Auana!
É a divisão da soma dos quadrados pelos respectivos graus de liberdade.
|Uau esse blog é magnífico , eu realmente gosto de ver seus posts. Continue o excelente trabalho! Você já sabe que, muitas pessoas precisam de posts sobre isso, você vai ajudá-los .
Acabei de conhecer este blog e estou achando show para aprender estatística!! Explicação simples e direta, parabéns para todos os responsáveis!! <3
Que ótimo! Ficamos muito felizes com seu comentário. Nosso objetivo é ensinar estatística de maneira simples e prática. Qualquer sugestão que tiver, fique a vontade para nos dizer! Abraço.
Informações valiosas! Muito obrigada.
Tenho uma dúvida: qual a melhor forma de apresentar os dados da ANOVA (tabela, boxplot)?
Oi, Andrea! Vai depender de como você quer passar a informação e para quem irá passar a informação. Por exemplo, a tabela/quadro da ANOVA apresenta todos os resultados, mas pode ser de difícil compreensão para quem não está familiarizado no assunto. Em contrapartida, o boxplot pode ser de mais fácil visualização e compreensão.
De forma geral, incluir tanto o quadro da ANOVA e quanto o boxplot são de grande importância, pois complementará mais na informação dos resultados. Vale ressaltar que a explicação dos resultados (seja do quadro ou gráfico) é o principal ponto.
Podemos definir da seguinte maneira:
Quadro: É como uma tabela com linhas e colunas, onde você pode colocar os números que representam as médias e outras medidas dos grupos, e também o resultado da ANOVA, que diz se as médias são iguais ou não.
Tabela: É parecida com o quadro, mas tem mais detalhes sobre como a ANOVA foi feita, como a soma dos quadrados, que é uma medida de quanto os dados variam em cada grupo e entre os grupos.
Boxplot: É um tipo de gráfico que mostra como os dados estão distribuídos em cada grupo, usando uma caixa com uma linha no meio. A caixa representa onde estão 50% dos dados, e a linha representa a mediana, que é o valor do meio. O boxplot também mostra os valores máximos e mínimos, e os valores que estão muito diferentes dos outros, chamados de outliers. O boxplot ajuda a ver se as médias e as variações dos grupos são parecidas ou não.
Gostaria de saber a melhor forma de apresentar os dados da ANOVA (quadro, tabela, boxplot?)
Gostaria de saber qual a melhor forma de apresentar os dados da anova? Quadro, tabela, bloxpot, grafico de barra?
Muito obrigada pelas informações
Bom dia,
O meu SPSS está apresentando a estatística Z em vez da estatística F. Qual é a diferença?
Deve ser apresentada da mesma forma? ex Z(1.31) = 31,319, p<o,001
Muito obrigado.
Bom dia, Paulo!
O comum é retornar a estatística F na ANOVA. Seria interessante você rever o passo a passo no SPSS, pois pode ter algum tipo de especificação errada, ou seleção errada do método no software.