O que é Modelagem de Equações Estruturais?

Pesquisadores têm utilizado ferramentas de análise estatística por muitos anos para ampliar sua capacidade de compreender e confirmar resultados de pesquisas. Uma dessas ferramentas é a modelagem de equações estruturais.

Com o desenvolvimento de hardwares e softwares, as aplicações dos métodos estatísticos cresceram exponencialmente. E muitos deles acabaram se tornando relativamente mais acessíveis com interfaces user-friendly, e conhecimento tecnológico integrado.

Os pesquisadores inicialmente utilizavam a análise univariada e bivariada para entender os dados e como eles se relacionam entre si. Para compreender relações mais complexas, é necessário aplicar métodos sofisticados de análise multivariada, que envolvem a aplicação de estatística.

Estes métodos mais sofisticados, como a Modelagem de Equações Estruturais, analisam simultaneamente múltiplas variáveis que podem ser métricas de: indivíduos, empresas, eventos, atividades, situações, etc. Essas métricas podem ser obtidas por meio de pesquisas e observações, que geram dados primários, ou pela coleta de dados secundários.

Os métodos estatísticos mais usados incluem não só abordagens baseadas em regressão – como regressão múltipla, regressão logística e análise de variância – mas também técnicas de análise fatorial exploratória, análise de agrupamento e escalonamento multidimensional.

Quando aplicados a um problema de pesquisa, esses métodos podem ser confirmatórios ou exploratórios. Especificamente, eles são confirmatórios ao testar as hipóteses de teorias e conceitos existentes à piori e são exploratórios quando eles identificam padrões de dados nos casos em que temos pouco ou nenhum conhecimento prévio sobre como as variáveis estão relacionadas.

A Modelagem de Equações Estruturais

A Modelagem de Equações Estruturais (SEM – Structural Equation Modeling) inclui um conjunto diversificado de modelos matemáticos, algoritmos de computador e métodos estatísticos que operam juntos para permitir aos pesquisadores incorporar conceitos não observáveis através de variáveis indicadoras medidas indiretamente.

Ele também facilita a contabilização do erro de medição nas variáveis observadas.

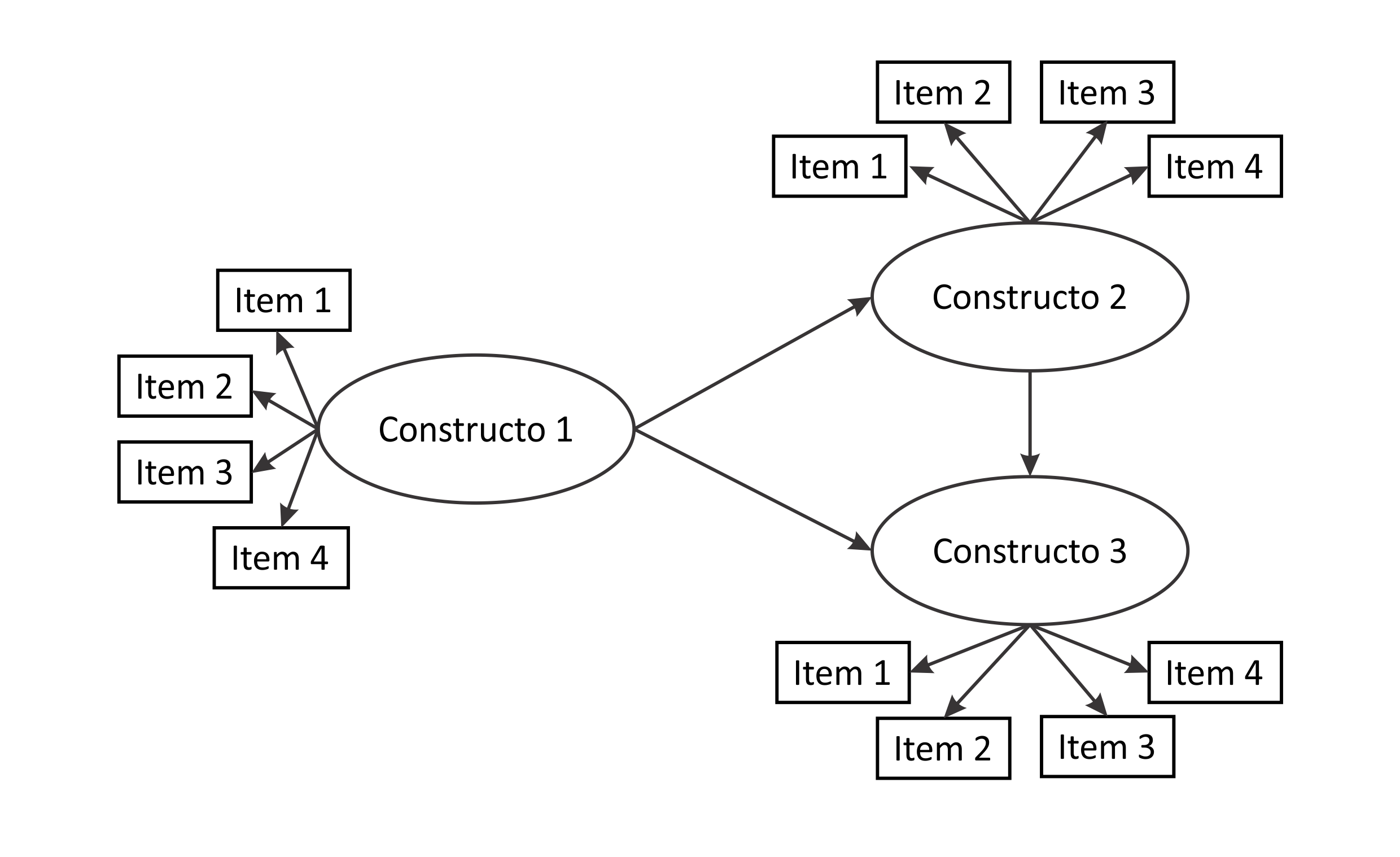
Exemplo de Modelo de Equações Estruturais

A Modelagem de Equações Estruturais é uma família de modelos estatísticos que busca explicar as relações entre múltiplas variáveis. Ela examina a estrutura de inter-relações expressas em uma série de equações, semelhante a uma série de equações de regressão múltipla. Tais equações descrevem todas as relações entre constructos envolvidos na análise. Constructos são fatores inobserváveis ou fatores latentes representados por múltiplas variáveis.

A SEM pode ser vista como uma combinação das técnicas de análise fatorial e análise de regressão múltipla.

As principais características

A SEM é conhecida por muitos nomes: análise estrutural de covariância, análise de variável latente, e, às vezes, simplesmente pelo nome do pacote especializado usado (Exemplo: LISREL, AMOS).

Apesar de existirem diferentes maneiras para testar as SEM, todos os modelos de equações estruturais são caracterizados por três aspectos:

1. Estimação de relações de dependência múltipla e inter-relacionada.
2. Uma habilidade para representar conceitos não observados nessas relações é corrigir erro de mensuração no processo de estimação.
3. Definição de um modelo para explicar o conjunto inteiro de relações.

Modelo de Equações Estruturais baseado em Covariância

(Covariance-based Structural Equation Modeling)

O SEM (CB-SEM) baseado em covariância é usado principalmente para confirmar (ou rejeitar) teorias, isto é, um conjunto de relações sistemáticas entre múltiplas variáveis que podem ser testadas empiricamente. Ele faz isso determinando o quão bem um modelo teórico proposto pode estimar a matriz de covariância para um conjunto de dados de amostra.

Modelo de Equações Estruturais via PLS

(Partial Least Square Structural Equation Modeling)

Em contraste, o PLS-SEM, também chamado de modelagem de caminho PLS, é usado principalmente para desenvolver teorias em pesquisa exploratória. Ele faz isso, concentrando-se em explicar a variância nas variáveis dependentes ao examinar o modelo.

Artigo desenvolvido com a colaboração de Luana Sílvia dos Santos

Referências:

Hair, J. F. J., Hult, G. T., Ringle, C. M. e Sarstedt, M.. A primer on partial least squares structural equation modeling (PLS-SEM). Sage Publications, 2016.
Marôco, J. Análise de equações estruturais: Fundamentos teóricos, software & aplicações. ReportNumber, Lda, 2010.