A estatística é uma ciência interdisciplinar cujos métodos contribuem para o avanço das demais. A análise de sobrevivência, utilizada para estimar o tempo até a ocorrência de determinado evento, é muito empregada pelas ciências da saúde, biológicas e engenharias.
Qual o tempo estimado para a cura de pacientes submetidos a determinado tratamento? Quanto tempo leva até um equipamento ou componente apresentar defeito? Quais fatores influenciam o tempo de recuperação de um paciente?
De certa forma, técnicas clássicas como a análise de regressão simples, podem ser utilizadas para responder a estas perguntas. Entretanto, é comum que o evento estudado não ocorra em alguns elementos amostrais. Como aproveitar essa informação censurada no meu modelo? É com o objetivo de tratar essas censuras que se utiliza a análise de sobrevivência.
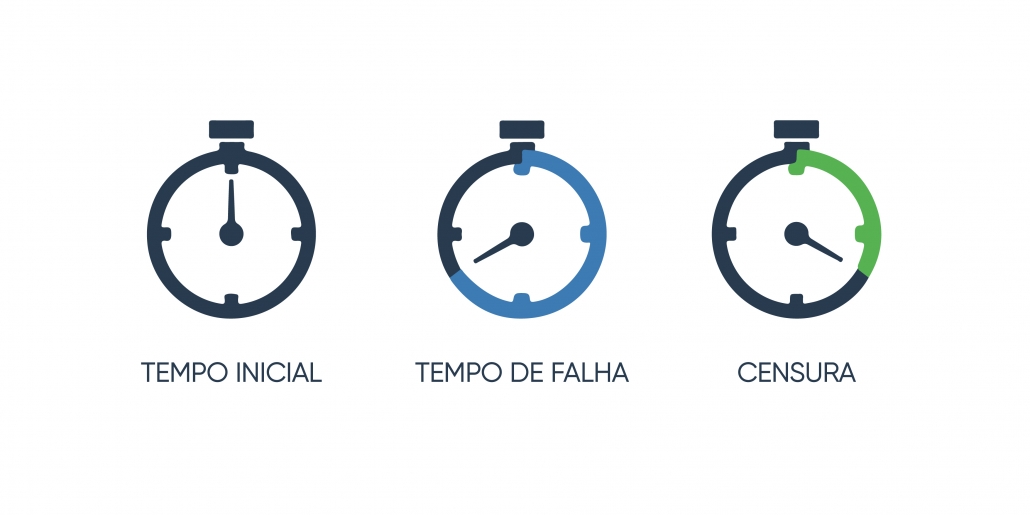
Tempo Inicial e Tempo de Falha
Em problemas práticos, geralmente não é possível coletar todos os dados ao mesmo tempo. Dessa forma, faz-se necessária a definição clara e objetiva do Tempo Inicial do estudo. Ele pode ser definido como data da primeira consulta, do início do tratamento, da primeira utilização de um equipamento, de fabricação de um componente, etc.
A partir da definição do Tempo Inicial, temos a variável resposta em análise de sobrevivência que é o Tempo de Falha. Ou seja, o tempo até a ocorrência de um determinado evento. A unidade de medida do tempo de falha também é uma característica importante no planejamento do estudo, podendo ser medida em horas, dias, meses, anos, etc.
Censura
A presença de censura caracteriza os modelos de análise de sobrevivência. Censura pode ser definida como a ausência da ocorrência do evento no tempo de análise. Ou seja, por motivos que não envolvem o objetivo central do estudo, o elemento amostral não apresenta tempo de falha.
Razões usuais para a censura podem ser o tempo restrito de acompanhamento, a impossibilidade de um paciente continuar a participar do estudo, substituição de um equipamento, etc. O tempo até a ocorrência da censura também é registrado e levado em consideração nos modelos de sobrevivência. Ele se caracterizando em geral como o último registro do acompanhamento do elemento amostral.
Exemplos de aplicação da análise de sobrevivência
Suponhamos que seja de interesse de um pesquisador medir os fatores de influência no tempo até a cura de uma enfermidade em pacientes submetidos a determinado tratamento. Suponhamos ainda que 72 pacientes foram acompanhados por dois anos desde o diagnóstico da enfermidade.
Neste cenário, o Tempo Inicial de análise é marcado pela data do diagnóstico da enfermidade e o tempo de acompanhamento é registrado em meses. Dessa forma, o Tempo de Falha é o número de meses até o diagnóstico de cura do paciente. Durante o período do estudo, pacientes podem mudar de endereço sendo alocados em outra unidade de saúde, não podendo assim ser acompanhados. Outros podem sofrer acidentes fatais durante o período ou simplesmente deixar de ir às consultas. Esses casos seriam tratados como Censuras.
Vamos supor agora que o objetivo de uma fábrica seja aumentar sua produtividade. Para isso, se propôs a criação de um programa de manutenção preventiva nas máquinas de embalar. O objetivo desse programa era diminuir a ocorrência de falhas e o tempo com máquinas paradas.
Para isso, define-se como Tempo Inicial de análise a data da última manutenção realizada nas máquinas de embalar. Assim, o Tempo de Falha seria o número de horas de produção até a interrupção por falha. A substituição de uma máquina ou sua interrupção proposital, devido à redução da produção, por exemplo, poderiam ser tratados como Censuras.
Função de Sobrevivência e o Estimador de Kaplan-Meier
A Função de Sobrevivência – S(t) é definida como a probabilidade de sobrevivência de uma observação até um certo tempo t, ou seja, a probabilidade de uma observação não falhar até o tempo t. Uma técnica amplamente utilizada na estimação de S(t) é o Estimador de Kaplan-Meier.
O Estimador de Kaplan-Meier é definido a partir de uma técnica não-paramétrica e é muito utilizado nas ciências da saúde, biológicas e engenharias. Nela a função de sobrevivência S(t) é caracterizada como uma função escada com degraus nos tempos observados de falha. Como pode ser observado na figura abaixo, um “degrau” representa a ocorrência do evento e o tamanho do degrau é proporcional ao número de eventos ocorridos. O símbolo de “+” representa o tempo de censura de uma observação.
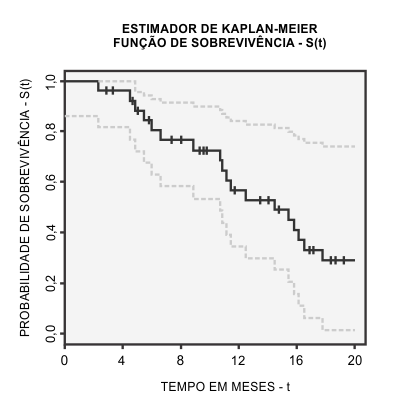
A partir do Estimador de Kaplan-Meier é possível comparar os tempos de falha segundo variáveis qualitativas. No exemplo citado anteriormente, pode-se comparar o comportamento do tempo até a cura do paciente de acordo com outras variáveis de interesse, como sexo, idade, obesidade, tabagismo, etc.
Exemplos
Por exemplo, pode-se estimar o Estimador de Kaplan-Meier separadamente para homens e mulheres e comparar as curvas de sobrevivência. Além da análise visual, é possível testar a significância da diferença entre as curvas de sobrevivência utilizando o teste logrank.
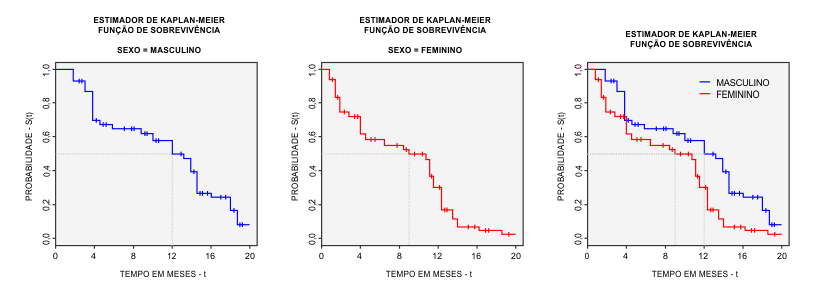
Ainda, utilizando o Estimador de Kaplan-Meier é possível estimar o tempo mediano e médio de sobrevivência. O tempo mediano de sobrevivência é indicado pelo tempo t onde S(t) é igual a 0.50. Como pode ser observado nos gráficos acima, o tempo mediano de cura dos pacientes do sexo feminino é 9 meses e do sexo masculino é 12 meses.
O Estimador de Kaplan-Meier é muito útil na avaliação individualizada dos fatores de influência sobre o tempo de falha. Entretanto, para a avaliar conjuntamente múltiplos fatores, faz-se necessário o uso de técnicas mais sofisticadas, como os modelos de regressão para sobrevivência.
Modelo de Regressão de Cox
A Regressão de Cox ou Modelo de Riscos Proporcionais é bem flexível na modelagem de dados de sobrevivência. Cox modela a taxa de falha entre as covariáveis e a interpretação dos coeficientes dá-se pela Razão de Taxas de Falha ou Risco Relativo (R.R.). A interpretação do Risco Relativo (R.R.) é similar à da Razão de Chances (O.R.), da Regressão Logística.
O Modelo de Cox, que é semi-paramétrico, assume que as taxas de falhas são proporcionais. Ou seja, o risco de falha das variáveis é constante ao longo do tempo. Por exemplo, o modelo assume que o risco de cura em indivíduos do sexo feminino em relação ao sexo masculino é constante em todo o período de acompanhamento do estudo.
Vale ressaltar a importância de se verificar a adequação do modelo e para isso existem várias técnicas que poderão ser abordadas futuramente.
Modelos de Regressão Paramétricos
Uma alternativa ao Modelo de Cox são os modelos lineares para dados de sobrevivência. A utilização de técnicas paramétricas, quando bem ajustadas, apresentam melhores resultados em relação as técnicas não-paramétricas, apesar de não serem tão flexíveis.
Os modelos paramétricos assumem uma distribuição de probabilidade para o tempo de falha, sendo as distribuições Exponencial, Weibull e Log-Normal as mais comuns. Estes modelos são baseados na estimação da razão de tempos medianos de sobrevivência.
Como utilizar a análise de sobrevivência?
A maioria dos ambientes e softwares de análise estatística possuem recursos para se estimar os modelos de sobrevivência. O R, por exemplo, possui pacotes específicos para a análise de dados de sobrevivência.
Ainda com dúvidas sobre os métodos de análise de sobrevivência? Gostaria de uma orientação sobre como utilizá-los em seu projeto de pesquisa ou em sua empresa? Entre em contato com nossos Data Talkers e não deixe de inscrever para receber nossas futuras publicações.
Artigo desenvolvido com a colaboração de Leonardo Gonçalves.




2 comentários em “O que é análise de sobrevivência?”
ola bom dia somente uma duvida em relação a censura se pode ser aplicada.
Por exemplo tenho dois laudos que estam buscando uma leito. Um por razoes particulares se torna judicializado e outro não é e quero medir o tempo de ambos. posso considerar que um possui censura
Oi, Douglas! Se os indivíduos não participarem do evento de interesse (ou seja, não ocorrer o evento de interesse com os indivíduos do estudo), por motivos diferentes do estudado, pode ser considerado censura. Por exemplo, se um indivíduo sai do estudo por alguma causa atípica e que não é referente ao evento de interesse, ele pode ser considerado censura.